Prove All Polynomials Are Continuous on R
Get the answer to your homework problem.
Try Numerade free for 7 days
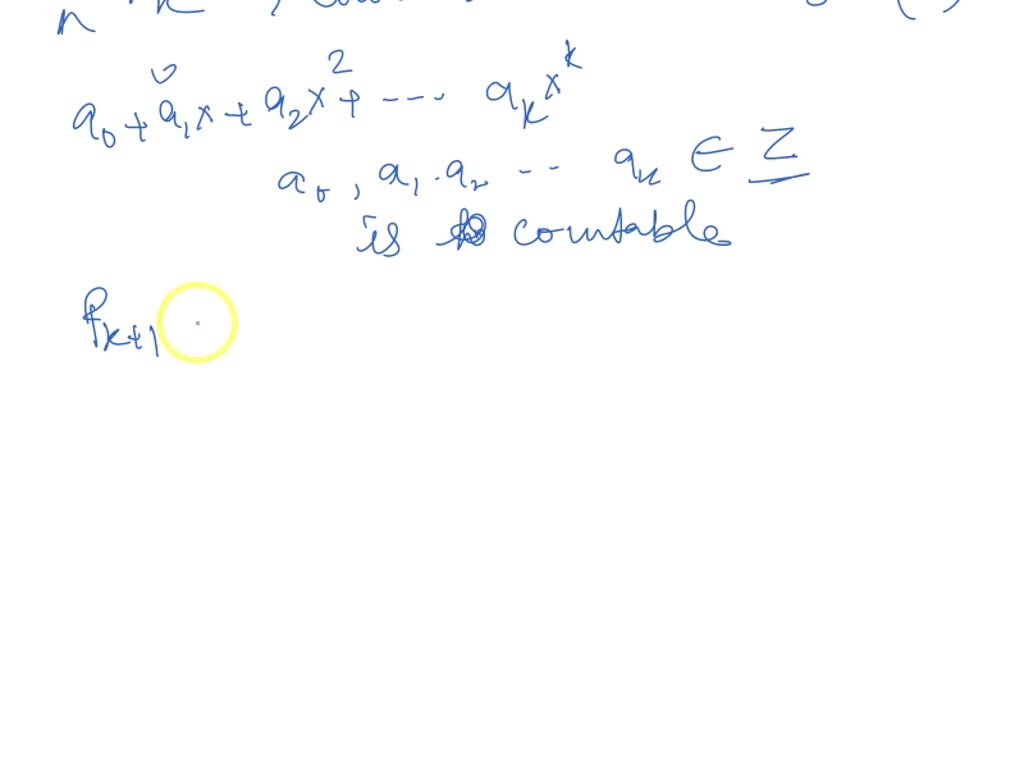
Prove that all polynomials are continuous on R Hint. Induction on the degree.
Related Question
with integer coefficients. Prove that Pn is Let P be the set of all polynomials of degree n countable (Hint: consider proof by induction)
Discussion
You must be signed in to discuss.
Video Transcript
high in the given problem. It is given that PM is a polynomial of degree N. So here we have to prove that this is countable by using mathematical induction. So we'll start with taking p. one. So P one is a set of the paranormal with degree one. And this satisfied the condition on P. N. And this is countable. Now here Let P one let everyone belongs to all the interior Zet cross said. Such that I am not plus a one X. So this is the polynomial degree one is all belongings to a naught comma even with a not anyone even other coefficient. Clearly this map to 1- one. So this is one. So it means that since so this will be accountable. Health. We can say that said Israelis constable. Soapy one is countable. Now coming to the second part will assume that P. K is countable. Well just because we have just proved that P one is countable. So we will assume that P. K is countable. Now PK is a polynomial with degree K. The greek. So we'll write this Parliament P. K. This is not Plus A one X plus a two X squared plus up to ak X. To the power. So that's the problem of degree case. Such that A one A two up to ak not he won a two up to ak there belongs to the teacher said. And this is countable. Hence this is countable. So because that is accountable here. Now if we if we prove to prove. So if he can prove that B. K plus one is also comfortable, then we can prove that PN is comfortable. Hence we can prove that P N is countable. Now P K is the is the polynomial with degree K. So this is a degree K plus one. So this polynomial can be written as in order to bless even X plus eight X squared two. A extra the power gay plus AK- Plus one extra. The power K plus one. We're not even we're in our you in a two up to eight about a K plus one. They all belongs to set. So we can write this as this has a not plus even X plus a two X squared to a power as. So we'll take this as you. So let's say this is you. So let this is you. So this whole thing will become you plus. So this is PK P K. U plus AK- Plus one. A K plus one extra the power K plus one. Now hear this expression it K plus one extra K plus band. Where a K plus one belongs to Z. K-plus one belongs to the same as I had same accountability as it. So by assumption we have assumed that P K is countable. So we know that the union of accountable to the accountable is countable. So we can say that hence P K plus one is PK. You. And this implies that a K plus one comma X X to the power Extra about K-plus one is also belonging to zero, and this is countable. So hence by mathematical induction, we can say that P n is a polynomial such that p n is countable. So that's a complete solution. Thank you.
Source: https://www.numerade.com/ask/question/prove-that-all-polynomials-are-continuous-on-r-hint-induction-on-the-degree-86295/
0 Response to "Prove All Polynomials Are Continuous on R"
Post a Comment